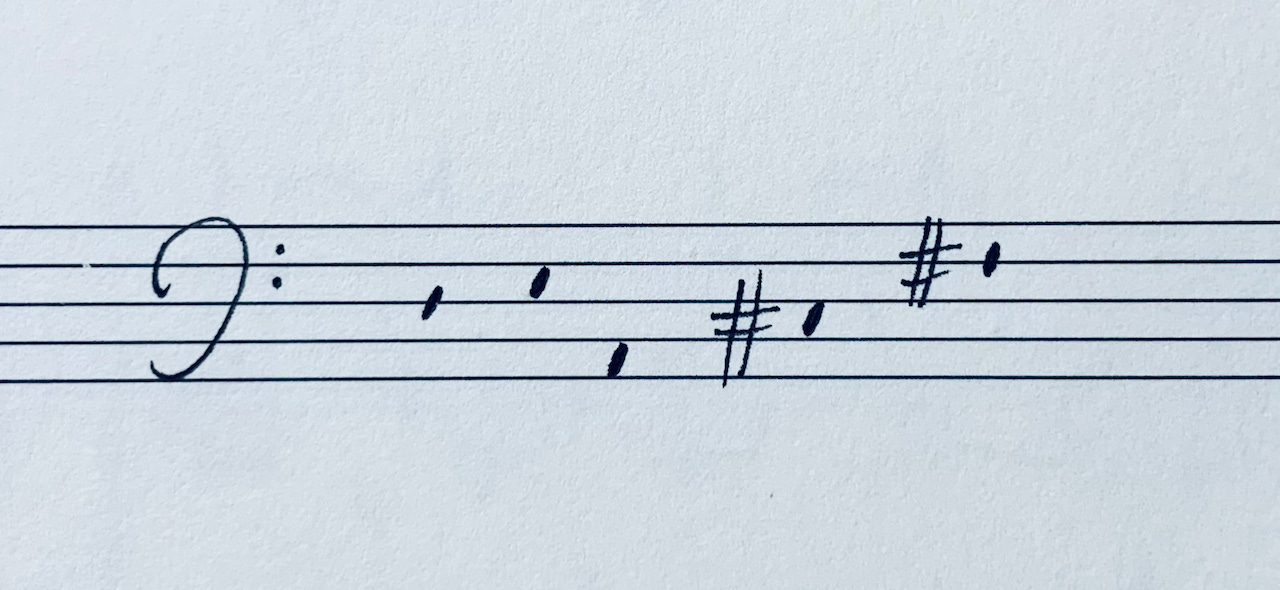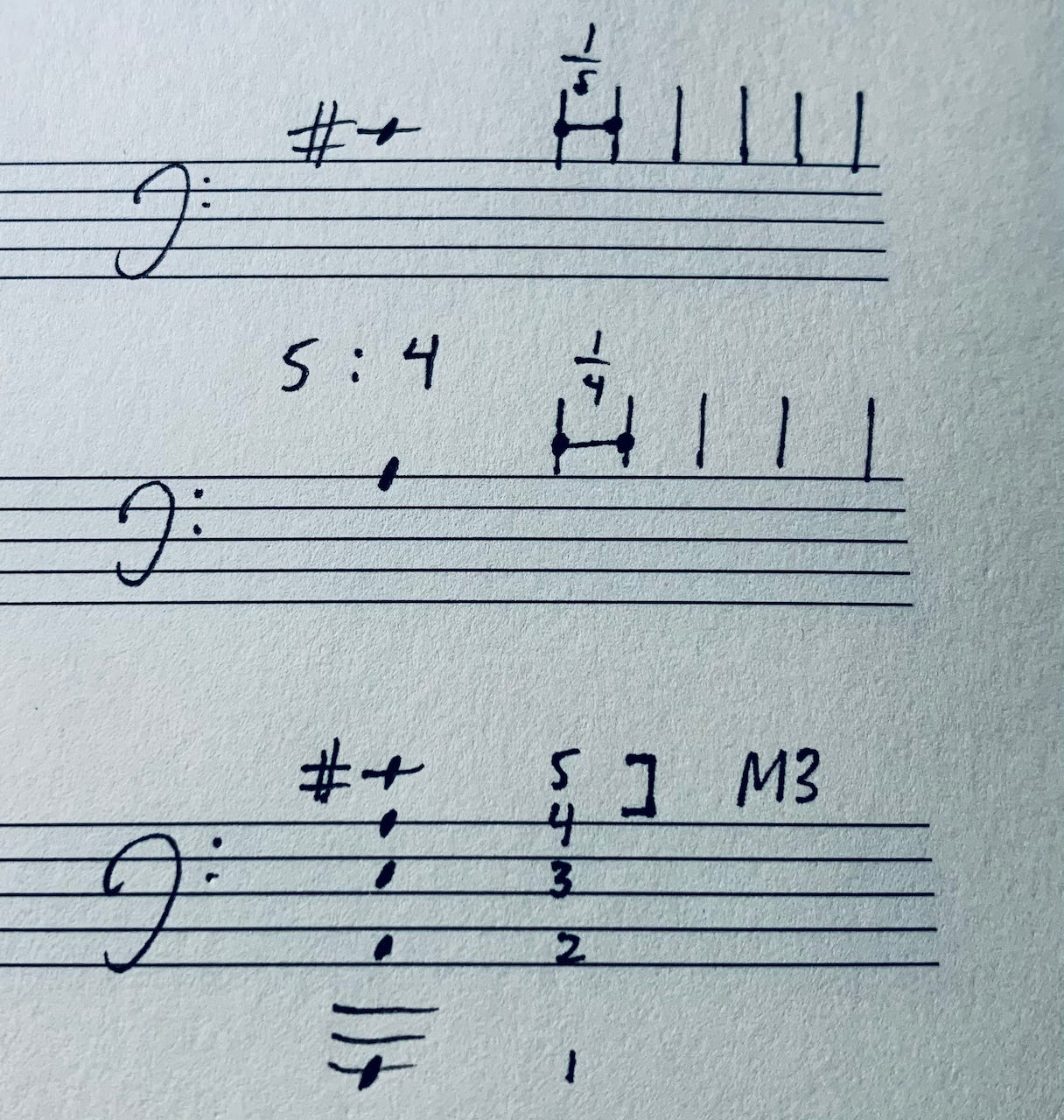Day One: Musical Sound

Sound, Fundamentals, and Overtones

You can develop a deeper connection with sound by understanding the overtone series as the basis of musical organization.

Laws of Sound

Our discussion of harmony begins with the physical qualities of sound and the musical consequences of those qualities. The laws of physics and acoustics will definitely interest a musician studying theory and harmony. Closely investigating the phenomena is how we will come to learn about the possibilities of sound, and ultimately find the roots of music in the laws of nature. This approach doesn't reduce music down to the level of science, but rather elevates it to the highest level of artistic potential by making the effect that it has on us comprehendible. The goal for studying harmony is to gain mastery over the raw materials of music so that we may eventually use it to build and exteriorize that which moves inside us. 

Figure 1.

What are the building blocks of music? Tones are the material that music is made of. Pieces of music are fabrics of tones arranged and woven together by a musician. When we open a musical score, or see music on a staff, we are actually looking at sound. The translation from the dead page to the life of the musician is absolutely key—without it music doesn't happen. A major goal for today is to awaken many of the unconscious processes that happen during this translation, starting with the phenomena of hearing tones. 

A tone is a sonic unity. Tones are actually made up of an infinite number of parts, which can be broken down into two categories. The sonic entity we know as a tone is composed of a fundamental vibration and its series of overtones. The fundamental is a stable and steady vibration, one that is regular and repeating. The musical tones are the sonic opposites of noise, which are irregular, non-repeating sounds. I use tone and sound pretty interchangeably in my speech and writing, but the sound that I have in mind is a musical tone, not noise. This regular repetition that gives the tones their character is important to keep in mind since that's what distinguishes them from everything else we hear. Consider walking down the block, and you hear the voice of a singer that causes you to pause—the tones pull you out of the world for a moment—you hear a striking and fundamental contrast to the noises that color our everyday experience.

Figure 2. A piano tone sounding on Fifth Ave.

Listen closely to the tones that surround you. Pluck your guitar string, play a long tone on your sax, or even better just sing a note, and take a moment and listen and let the sound evolve in your mind. If the tone is unchanging, meaning that it isn't raising or lowering in pitch, then the vibration is stable and allows for the natural presence of the overtones—the new and higher tones that you are hearing. The truth is that those higher tones were always present, and they emerge due to no will of ours. The higher tones, or overtones, are themselves birthed by the fundamental via its own vibration. The richer the sound, the more audible the overtones. By using this experience and zooming in to sound, we find a structure that is given to us by Nature.

Figure 3. The difference between the harmonics and the overtones is that the first note of the harmonic series is the fundamental, and the first overtone is the second harmonic. 

At the heart of every tone is the harmonic series, which is composed of a fundamental and its series of emergent new tones, the overtones. The whole series sounds together at the same time, and theoretically continues infinitely. The tones that appear early on in the series are closer to the fundamental in pitch and sound louder—the fundamental is the loudest sound heard. As you ascend the harmonic series the tones become weaker in volume, so in practice it’s only useful to work with the first 7 or 8 overtones, shown by Figure 3. 

This natural and audible structure is remarkable because it unites abstract concepts such as number and proportion with our inner world of experience through our sense of sound. The new tones can be mathematically derived with a beautiful and simple pattern that relates each overtone with the fundamental—and the musical consequences of these mathematical relations is as remarkable as the structure itself. Every note in a piece once in motion has this entire structure at its core.

Sound-Relations

Figure 4.

How do the tones relate to each other in nature? Each note contains a family of other notes that are in a very concrete relation to it. 

The overtones strengthen and give stability to the fundamental. Each new tone in the series can be known and understood and lived as the musical intervals.

Figure 5. The overtones emerge as fractional proportions of the fundamental. 

How do the intervals articulate inside the overtone series? One way to understand the harmonic series is by looking at the intervals between the overtones as fractions, or partials, of the vibrating piano string. The simple pattern is as follows: the first harmonic is 1/1, the whole vibrating string. The second harmonic is 1/2, half the string is vibrating. The third harmonic is 1/3, vibration of a third of the string. And so forth; the harmonics spell out one of the most beautiful patterns in nature! 

As you ascend the series, each new tone is an interval away from the previous tone. The first interval that appears is the Octave, between harmonics 1 and 2. The next interval is between harmonics 2 and 3 and is the Fifth. Between 3 and 4 is a Fourth, between 4 and 5 a Major Third, 5 and 6 a Minor Third, between 6 and 7 is an even-smaller minor third*, and between 7 and 8, a Major Second. The series continues to extend infinitely with increasingly smaller and smaller intervals, eventually crossing into microtones beyond the limit of perception. 

Each new tone is a smaller fraction of the vibrating string. Each higher tone is quieter than the last. Tones that are closer to the fundamental are louder and more a part of the overall sound. Timbre is the additive result of the volumes of each of the overtones.

The Musical Ratios

Octave 1:2

Fifth 2:3

Fourth 3:4

Major Third 4:5

Minor Third 5:6

Smaller minor third* 6:7

Major Second 7:8

*A note about the “smaller minor third.” The tones and intervals that appear in the harmonic series are born out of perfect mathematical proportions and don’t exactly fit into our calibrated equal tempered tuning system. That’s why the actual tones of the overtone series sound slightly out of tune to our ears.

The main lesson here is that the intervals appear as concrete ratios, proportions, born out of the natural harmonic series. The intervals are given by the series itself. 

We will go in depth with the intervals and combinations of tones in a musical context on Day 3 of the course. But for now, we will look at the intervals more objectively: as they appear in the harmonic series. 

Here is how to visualize any musical ratio using the fractional string lengths. We'll take the 4:5 ratio of a Major Third as the example, between A and C# (harmonics 4 and 5 from Figure 5). As you can see, it is 1/4th of the string sounding with 1/5 of the same string: concrete proportions made into sound. 

Figure 6. Precise math sounds good. 

Major 3rd

Laws of Music

What does all of this mathematical patterning and observation have to do with musicality? In one word, the answer is stability. In music the concepts that we may take for granted—establishing a tonic or departing from one, phrasing and cadencing, voicing—all more or less have to do with stability of sound.

For one, tones are very stable sounds by themselves; they derive their strength from other pitches that it itself creates. In nature the fundamental and its enriching overtones are inseparable. But there is much more to it than that. We actually have learned about harmony by examining the harmonic series. 

Look at harmonics 4, 5, and 6. They are all close to the fundamental and are easily heard new tones that live inside each note. The strongest overtones that enrich the fundamental form a major triad: the tonic (fundamental), major third, and perfect fifth. 

The stability and finality of the major chord has its root in the fact of harmonic vibration. More importantly, if we define harmony as the study of simultaneously occurring tones, then each note contains a universe of stable and "pre-ordained" harmony inside of it. (Bonus point if you can identify which conductor famously referred to the harmonic series as the "built-in pre-ordained universal.")

Figure 7.

Furthermore, the intervals are given by nature and can therefore be approached and studied as natural phenomena. These two acoustical facts enrich our understanding of music and allow us to approach music with a much deeper understanding. By simply taking the time to hear sound in its full richness, one opens the door to a much wider perspective of music making which embraces the entire potential of sound, and not just the surface level of fundamental tones, the dots we see on the page.

Now that we've glimpsed into the literal hearts of every musical note, listened to sound with our full consciousness, and saw a universal pattern, we can start to see where music gets its power from. After all, music appears to us as some of the most subjectively moving experiences. How can ephemeral tones create those undeniable moments of timelessness, these expanding unforgettable moments of great beauty? 

Figure 8. Movement from C to D is more than it seems at first.

Tones don’t exist without a family of other simultaneous tones that give the fundamental its essence. Taking what we've learned and applying it to this simple movement from C to D, we can see that there is actually a battle, a clash of the overtones, of one total richness against another. 

Most importantly, these intervallic proportions can be lived. Our ears “sieve” and measure sounds and hear in a precise way: all of us will agree that the movement is a Major Second. The overall and total effect of this sound, moving from C to D, is musical tension that invokes the melodic force which moves the spirit, my inner life, in a concrete way. In other words, I become aware of the Major Second. 

To resolve this tension, I can fall a Fifth to G. Then I can raise a Fourth to complete the phrase. The family in G supports the family in C; G brings the ear nearer to C. The overtones (combined with the intervals themselves, as we'll see on Day 3) all work together to resolve the tension of the first interval, completing the phrase. This universality is one of the elements that separates music from the rest of the arts, which all have their models in the physical world.

Figure 9.

Once we get a sense of the inner life behind the notes we can start to make music differently. Each connection of notes is an opportunity to observe the effect that sound has on our living experience. The work begins with the musical consciousness in contact with the unique sound created in each moment. In my experience the impact becomes more direct, and we can translate our inner worlds with tones and timing and phrasing much more effectively through this practice. 

As practicing musicians we will inevitably create our own paths. When we learn harmony traditionally we learn historic styles of writing music. Our aim must be to find how each of the notes relates to the others so that we can freely use them. As long as we work with sound we must familiarize ourselves with its richness to learn that it is its own source of harmony. 

Develop a deeper connection with sound by understanding the overtone series as the basis of musical organization: A summary.

1. The richness of sound provides the basis for tonal organization. New tones emerge from fundamental tones, and they can be ranked based on how closely related they are to the fundamental given by their order of appearance and strength in the overtone series. Coming to know the richness of sound is to listen with our whole being and discovering the properties and effects of sound. The way we approach listening determines the way we shape the notes in our music making.

Figure 10.

2. The notes relate to other notes in a concrete way. The same tone can appear in different contexts, for example, the same octave C appears as different harmonics above several other tones. Understanding and living the relationships through working with the intervals is key.

Figure 11. The octave below sign (8vb) just applies to the fundamental tones.

3. It is possible to relate all 12 tones of the chromatic scale to a fundamental sound based on how 'near' the tones are relative to the fundamental. This is a new way of approaching harmony, free from diatonic scales, and based on the richness of sound. We know the notes that are close to C are G, E, A, F, Eb, Bb, Ab. But how? They are related based on the overtones that they share. In The Craft of Musical Composition, Hindemith ranks the 12 notes of the chromatic scale based on their tonal significance and value to a fundamental in a new series based on how the harmonics overlap. Consider that G is the upper fifth of C, and that C is the upper fifth of F, making them both close to C even though F does not appear audibly in the harmonic series of C. Similarly, A is close to C since they both share E, being the 3rd harmonic of A and the 5th harmonic of C. 

Figure 12. Series 1 from Hindemith’s Craft of Musical Composition. 

4. These relations have concrete impacts on our consciousness. The fact of an Octave, of a Third, is beyond mere emotions. Experiencing them creates sensations inside of us, and moves us all similarly. 

The ear hears simple ratios as stable and beautiful.

Figure 13.

Building One Sound, Then Two.

The next two weeks will definitely be an exciting one as we venture into music and all of its possibilities. Discussing music is always an opportunity to come together.

For the day 2 exercise we will be diving into some examples of the overtone series as they appear in the music of different composers. Then we’re breaking down the series and discovering for ourselves a remarkable pattern that governs the world of sound.

That will lead us into the next lesson where we get up close and personal with the intervals: the smallest units of music.

This post is part of 14 Days of Harmony, a free course for musicians who want to deepen their understanding of harmony, and learn how to develop their connection with sound as a result. You can view the entire course here.

Next day: The Overtone Series